SrideeStudio/Shutterstock
O ensino de matemática nas escolas está preso ao passado. Um adulto que revisitasse a escola que frequentou quando criança veria apenas mudanças superficiais em relação ao que ele mesmo vivenciou.
Sim, em algumas escolas, eles podem ver uma sala cheia de tablets eletrônicos ou o professor usando um quadro interativo sensível ao toque. Mas se nos concentrarmos nos detalhes – as tarefas e exercícios que os alunos estão realmente recebendo para ajudá-los a entender a matéria -, as coisas não mudaram praticamente nada.
Nos últimos anos, aprendemos muito sobre ciência cognitiva, como nosso cérebro funciona e como as pessoas aprendem de forma mais eficaz. Essa compreensão tem o potencial de revolucionar o que os professores fazem nas salas de aula. Mas a criação de materiais de ensino de matemática, como livros didáticos, tem se beneficiado muito pouco desse conhecimento.
Parte desse conhecimento é contraintuitivo e, portanto, é improvável que seja aplicado, a menos que seja feito de forma deliberada. O que os alunos preferem experimentar e o que os professores acreditam ser mais eficaz, muitas vezes, não é o que mais ajuda.
Por exemplo, a ciência cognitiva nos diz que a prática de tipos semelhantes de tarefas em conjunto geralmente leva a um aprendizado menos eficaz do que a mistura de tarefas que exigem abordagens diferentes.
Em matemática, a prática de tarefas semelhantes em conjunto poderia ser uma página de perguntas, cada uma delas exigindo a adição de frações. Misturar as coisas pode envolver a combinação de frações, probabilidade e equações em uma sucessão imediata.
Os alunos cometem mais erros ao fazer exercícios mistos e provavelmente se sentirão frustrados com isso. Portanto, agrupar tarefas semelhantes provavelmente será muito mais fácil para o professor gerenciar. Mas os exercícios mistos proporcionam ao aluno uma prática importante para decidir qual método deve ser usado para cada pergunta. Isso significa que mais conhecimento será retido posteriormente, o que é conhecido como “dificuldade desejável”.
Ciência cognitiva aplicada
Estamos apenas começando a aplicar descobertas como essas da ciência cognitiva para projetar materiais didáticos melhores e dar apoio aos professores para usá-los. O foco na matemática escolar faz sentido porque a matemática é uma disciplina obrigatória que muitas pessoas acham difícil de aprender.
Normalmente, os materiais didáticos escolares são escolhidos por reações instintivas. Um chefe de departamento examina um novo esquema de livro didático e, com base em sua experiência, escolhe o que lhe parecer melhor. O que mais se pode esperar que ele faça? Mas mesmo os melhores materiais oferecidos geralmente não são projetados tendo em mente os princípios da ciência cognitiva, como as “dificuldades desejáveis”.
Meus colegas e eu temos pesquisado design educacional que aplica princípios da ciência cognitiva ao ensino de matemática e estamos desenvolvendo materiais para escolas. Esses materiais não foram projetados para parecerem fáceis, mas para incluir “dificuldades desejáveis”.
Eles não são divididos em lições individuais, pois isso pressiona o professor a seguir em frente quando o relógio indica, independentemente das necessidades dos alunos. Ser sensível ao desenvolvimento da compreensão e das dificuldades dos alunos requer materiais projetados de acordo com o tamanho das ideias, em vez do que caberá convenientemente em uma página dupla de um livro didático ou em um período de aula de 40 minutos.
Mudando as coisas
Adotar uma abordagem orientada pela ciência cognitiva também significa mudar a forma como os conceitos matemáticos são explicados. Por exemplo, os diagramas sempre foram uma característica proeminente do ensino da matemática, mas muitas vezes são usados de forma aleatória, com base na preferência pessoal do professor. Nos livros didáticos, eles são altamente restritos, devido às limitações de espaço.
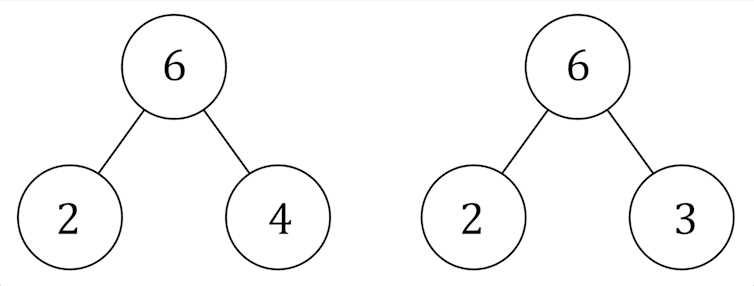
Muitas vezes, diagramas de aparência semelhante são usados em diferentes tópicos e para finalidades muito diferentes, o que gera confusão. Por exemplo, três círculos conectados como mostrado abaixo podem indicar a partição em uma soma o “modelo parte-todo”) ou um produto de fatores primos.
Isso envolve duas operações muito diferentes, mas são frequentemente representadas pelo mesmo diagrama. O uso do mesmo tipo de diagrama para representar operações conflitantes (adição e multiplicação) leva os alunos a confundi-las e a se confundirem.
Colin Foster
O “princípio da coerência” da ciência cognitiva significa evitar diagramas quando suas desvantagens superam seus benefícios, e usar diagramas e animações de forma intencional e consistente em todos os tópicos.
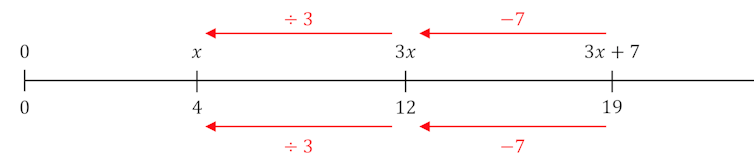
Por exemplo, as linhas numéricas podem ser introduzidas em uma idade jovem e incorporadas em muitas áreas temáticas para dar coerência ao entendimento que os alunos estão desenvolvendo sobre números. As linhas numéricas podem ser usadas para resolver equações e também para representar probabilidades, por exemplo.
Diferentemente dos diagramas circulares acima, os usos das linhas numéricas mostrados abaixo não entram em conflito, mas se reforçam mutuamente. Em cada caso, as posições na reta numérica representam números, do zero à esquerda, aumentando para a direita.
Colin Foster

Colin Foster
Combatendo desigualdades
Há desigualdades preocupantes no aprendizado da matemática, com alunos de origens mais pobres tendo um desempenho inferior ao de seus colegas mais ricos. Há também uma enorme diferença de participação de gênero em matemática, no nível médio e além, que é cursada por muito mais meninos do que meninas.
As famílias socioeconomicamente favorecidas sempre puderam ajudar os filhos para que não tivessem dificuldades usando professores particulares, mas as famílias menos privilegiadas não podem. Materiais didáticos de melhor qualidade, com base em percepções da ciência cognitiva, atenuam o impacto no aprendizado da matemática para os alunos que, tradicionalmente, são prejudicados por gênero, raça ou situação financeira.![]()
Colin Foster, Reader in Mathematics Education, Loughborough University
This article is republished from The Conversation under a Creative Commons license. Read the original article.


